“是我在梦中邂逅了这个世界，抑或世界原本就是我的梦？蝴蝶是我，抑或我就是蝴蝶？”

“从有记忆起，我所梦见的一切，最终都能从无中生出有，化为现实。这或许是很了不起的能力，但旁人都以异类的眼光看着我。我空想出了庞大的异界，却没有一个地方可以让我安放它。”
“在梦里，我曾经化身大鹏，飞往九万里的高空。从那里，可以看到世界浮沉于星海之上，渺小如同沙砾。它们诞生，发出夺目的光彩，转瞬之间又消失掉。”
“还做过一个漫长的梦，那是很久很久以前，遥远的时代，满眼令人惊异的景象：高耸入云的建筑栉比鳞次。不用马拉的车子飞速穿梭，长翼的铁鸟轰鸣着从头顶掠过。”
“人生有涯，而梦，无边无际。”

题目简介

本题共有1198人围观，最终只有1支团队攻破成功。在比赛过程中各个战队为了这道题百思不得其解，最终辣鸡战队勇夺一血，也是唯一攻破此题的队伍。

攻破此题的战队排名一览：

这道题难度实在太大，接下来我们一起来看一下这道题的点评和详细解析吧。

看雪评委crownless点评

本题的设计理念是题目即游戏。游戏分为两关，不同答案会根据通关情况给出不同的反馈，从而降低玩家的枯燥感。第一关把用户的输入限制到了很小的范围。第二关则验证了是否为唯一解。

出题团队简介

本题出题战队 兔斯基保护协会：

兔斯基保护协会团队成员只有大龙猫一个人，但依然出了难度很高的题，下面是相关简介：

队长和全部队员就是：大龙猫，如果不算上兔斯基的话。大龙猫，吉林四平人士。毕业于浙江大学计算机专业。热爱游戏、二次元、美食、画画和工作永远用不上的理论数学和物理。主业从事养兔斯基、windows逆向研究和软件对抗，业余挖洞。打红警能单挑四家凶残。此次比赛，感谢老婆对我的大力支持，老婆永远是我的女神！兔斯基是大龙猫的爱犬，也是爱子！美照如下：

设计思路

本题的设计理念是题目即游戏。游戏分为两关，不同答案会根据通关情况给出不同的反馈，从而降低玩家的枯燥感。
正确序列号可以通过两关，程序显示：Right! You are very clever!
不正确但过了第一关，程序显示：Wrong! You are close to the result!
一关都没过，程序显示：Wrong!
第一关直接可以得到32的字节的key，不过这个key恐怕在小范围内有多解的可能，所以再由第二关从第一关的解中筛选中正确的唯一解。（如果最终多解，我女装自拍发到比赛群里）
第一关：
本题限定用户的正确输入必须是正好32个字节。
本人搞了包含10个指令的指令集，把用户的输入转换为指令序列，然后开始跑如下程序：

void Sort()
{
int loop = 1;
LOOP: // 第一层循环
g_i = 1;
while (g_i < g_a_count) // 第二层循环
{
int pos = 0;
while (pos < 32)
{
跑用户指令
}
}
loop = (loop + 1) % 128;
if (loop)
goto LOOP;
}

这个程序就是个排序算法，排序需要的两层循环都已经限定死了，用户只需要填充每次比较和交换的逻辑即可。
我会用256位乱序数据来测试排序算法的有效性。
由于指令集非常基础而繁琐，用户所能达成目的有需要在32个字节之内，所以用户几乎只能使用冒泡算法：

void DefaultSort()
{
两层循环
{
// user code starts
if (g_box[g_a[i]] > g_box[g_a[i + 1]])
{
int temp = g_a[i];
g_a[i] = g_a[i + 1];
g_a[i + 1] = temp;
}
// user code ends
}
}

一种巧妙压缩后的算法如下：（正好32字节，不需要空操作，我本人没有想到更短的写法）

F代表指令集解释函数，只支持10种指令。
void Sort()
{
int loop = 1;
LOOP:
g_i = 1;
while (g_i < g_a_count)
{
// code starts
// (g_box[g_a[i]]
// block A1 starts (4 bytes)
F(4);
F(5);
F(6);
F(2);
// block A1 ends
// g_box[g_a[i + 1]]
// block A2 starts (5 bytes)
F(1);
F(4);
F(5);
F(6);
F(3);
// block A2 ends
// if (g_box[g_a[i]] > g_box[g_a[i + 1]])
// block A3 starts (4 bytes)
F(7, OP_TEST);
F(8);
F(9);
// block A3 ends
// do exchange g_a[i] and g_a[i + 1] if needed
// set operation
// block B1 starts (2 bytes)
F(7, OP_XOR);
// block B1 starts
// exchange g_a[i] and g_a[i + 1] if needed
// block B2 starts (16 bytes)
F(4);
F(3);
F(0);
F(4);
F(2);
F(9);
F(3);
F(1);
F(4);
F(2);
F(9);
F(3);
F(0);
F(4);
F(2);
F(9);
// block B2 ends
// i++
// block C starts (1 bytes)
F(0);
// block C ends
// code ends
}
loop = (loop + 1) % 128;
if (loop)
goto LOOP;
}

这个算法的一些部分有变体，少部分可以交换顺序，比如A1和A2。但B、C部分已经极度压缩，变体会撑爆32字节的限制。（也许存在更多的变体，但总体可能性很少）
按照交换和规律，和变体的候选集，用户无论是人工操作，还是写个自动程序，穷尽之都不算复杂。
第二关：
第一关把用户的输入限制到了很小的范围。直接在第二关过一下标准的sha2，都可以验证唯一解了。
用户所需要做的就是第一关把可能的解列出来，人工还是自动程序看用户口味。我觉得直接人工更省力。

解题思路

本题解题思路由看雪论坛大龙猫提供：

下面有python源代码：python3直接可以跑，python2也许也可以，我没用啥高级函数。
源代码第一部分是，虚拟机和题目机制解说，源代码加注释。
源代码第二部分是，有效解（正确答案）的得出，解空间数学证明。
源代码第三部分是，解枚举自动机。

铺垫：我的程序极小，代码很短，没加壳，可以通过IDA静态分析得到题目的代码架构如下图：

推荐判断方法：（对于有协议分析或者数据结构分析经验的选手，更容易找到关键点）
1、可以分析出虚拟指令集，只有10种指令，而且非常简练（见下文python代码）。指令集只能访问其中两块内存，其中一块是128个范围为 0-127 的数字，无重复，记作数组A；另一块是范围 0-255 的数字，但只有128个，且无重复，记作数组B。
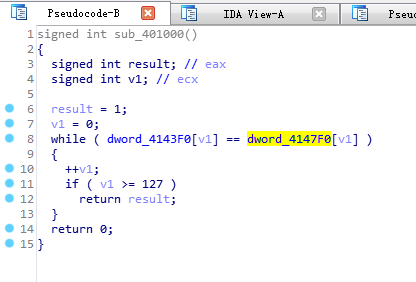
A和B在IDA中的位置见下图：dword_4143F0就是数组A，dword_413FF0就是数组B。

2、看结果判定的部分知，用于和计算结果比对的是一个由128个范围 0-127 的数字组成的数组，记作数组C。指令集不能操作数组C。
数组C在IDA中的代码位置如下图：

数组C在IDA中的内存如下图。是不是特征很明显？（我特意用int类型存放，以突出其是0-127的数组的特点。有数据结构逆向经验者，会觉得这比Offset+Length或者Length+Pointer的结构还明显，这就是个索引。当然，不需要这步就看出来，可以第3步再发现）

3、结合指令集的限制，和结果判断方式，我们主要研究A、B、C的关系，而这道题也明显应从数据特征分析入手。从A、C的构成来看，很明显有是索引的可能。用数组C的索引访问数组B，是升序排列。可见是个排序题。（总共就3块数据，来回排列组合式的看看关系，也能看到升序数列，有python代码清晰展示这三块数据的内容）

A = [29, 76, 10, 59, 66, 1, 94, 48, 6, 74, 40, 17, 81, 119, 3, 28, 2, 45, 75, 122, 126, 105, 107, 96, 36, 115, 71, 125, 64, 0, 41, 70, 9, 117, 92, 121, 7,
27, 95, 111, 78, 26, 16, 85, 104, 58, 8, 82, 124, 113, 18, 79, 99, 97, 88, 11, 24, 109, 108, 52, 46, 110, 93, 43, 30, 86, 37, 87, 31, 118, 62, 35, 38, 77, 14, 51, 47, 55, 57,20, 89, 69, 65, 39, 101, 103, 15, 60, 44, 102, 73, 23, 90, 22, 91, 13, 98, 120, 25, 19, 50, 112, 56, 42, 5, 123, 53, 127, 80, 32, 49, 34, 54, 61, 84, 83, 100, 33, 12, 114, 4, 21, 72, 116, 63, 68, 106, 67]
B = [64, 58, 59, 7, 49, 95, 141, 175, 31, 115, 45, 215, 226, 154, 250, 149, 182, 135, 187, 70, 114, 120, 105, 88, 15, 234, 18, 89, 216, 176, 75, 251, 97,
166, 46, 78, 225, 35, 124, 203, 252, 86, 138, 169, 196, 199, 238, 158, 171, 102, 177, 60, 100, 72, 82, 143, 13, 181, 210, 43, 159, 65, 222, 173, 101,
93, 168, 39, 185, 69, 79, 17, 198, 2, 61, 37, 218, 243, 133, 52, 213, 245, 4, 111, 121, 255, 20, 233, 76, 117, 40, 118, 19, 128, 241, 132, 244, 178, 62,
116, 206, 51, 148, 80, 211, 142, 204, 74, 209, 21, 230, 162, 130, 25, 190, 106, 108, 5, 249, 92, 29, 83, 155, 11, 205, 57, 248, 253]
C = [73, 82, 117, 3, 123, 56, 24, 71, 26, 92, 86, 109, 113, 120, 8, 37, 75, 67, 90, 59, 10, 34, 4, 101, 79, 125, 1, 2, 51, 74, 98, 0, 61, 69, 19, 53, 107,
30, 88, 35, 70, 103, 54, 121, 41, 23, 27, 119, 65, 5, 32, 52, 64, 49, 22, 115, 116, 83, 20, 9, 99, 89, 91, 21, 84, 38, 93, 112, 95, 78, 17, 42, 6, 105, 55, 102, 15, 13, 122, 47, 60, 111, 33, 66, 43, 48, 63, 7, 29, 50, 97, 57, 16, 68, 18, 114, 44, 72, 45, 39, 106, 124, 100, 108, 58, 104, 80, 11, 28, 76, 62, 36, 12, 110, 87, 25, 46, 94, 77, 96, 81, 126, 118, 14, 31, 40, 127, 85]
D = []
for i in C:
    D.append(B[i])
print(D) # 输出升序数列

4、由IDA分析到两重循环调用未知指令流，就知道要填写的代码仅仅是：if (比较){交换;} i++;（两重循环也是排序的特征，想到这个甚至可以跳过1、2、3步）

5、正确答案选取的是笔者认为最直接的思路，只要排序成功都能看到鼓励性输出。

6、笔者提供了自动机枚举答案的变体24640种，这些变体的大多数变体是有效但反人类的编程方式。笔者相信大多数人不需要机器枚举。
python程序只给了5个数据，原题是128个。不过，这完全不影响解法和解空间。

7、数学证明和编写思路见python程序的注释。

下面python程序正式开始：

# WP By Totoro 大龙猫
# GOAL: sort the g_box
g_box = [2, 1, 3, 5, 4]
defrecover_box():
global g_box
g_box = [2, 1, 3, 5, 4]
# The followings are the test functions. Our goal is to make function "test" return True!
defsort_wrapper(func, *args):
global g_box
global g_i
loop =1
while loop <5:
g_i =1
while g_i <5:
func(*args) # this is the user input
loop = loop +1
result = g_box.copy()
for i inrange(0, 5):
result[i] = g_box[g_a[i]]
return result
deftest(func, *args):
if sort_wrapper(func, *args) != [1, 2, 3, 4, 5]:
returnFalse
returnTrue
# The following is the description of the virtual machine I designed.
# virtual registers
g_i =1
g_value =0
g_op =0
g_op1 =0
g_op2 =0
g_less_than =0
g_a = [4, 2, 1, 0, 3]
# macros
OP_ADD =0
OP_SUB =1
OP_AND =2
OP_OR =3
OP_XOR =4
OP_TEST =5
OP_MAX =6
# virtual instructions
definc():
global g_i
g_i = g_i +1
defdec():
global g_i
g_i = g_i -1
defset_op1():
global g_op1
g_op1 = g_value
defset_op2():
global g_op2
g_op2 = g_value
defload_value_i():
global g_value
g_value = g_i
defload_value_mem():
global g_value
g_value = g_a[g_value]
defload_value_box():
global g_value
g_value = g_box[g_value]
defload_op(op):
global g_op
g_op = op
defreset():
global g_less_than
g_less_than =True
defcontitional_calculate():
global g_less_than
if g_less_than:
if g_op == OP_ADD:
g_a[g_op1] += g_a[g_op2]
if g_op == OP_SUB:
g_a[g_op1] -= g_a[g_op2]
if g_op == OP_AND:
g_a[g_op1] &= g_a[g_op2]
if g_op == OP_OR:
g_a[g_op1] |= g_a[g_op2]
if g_op == OP_XOR:
g_a[g_op1] ^= g_a[g_op2]
if g_op == OP_TEST:
if g_op1 < g_op2:
g_less_than =True
elif g_op1 == g_op2:
g_less_than =False
elif g_op1 > g_op2:
g_less_than =False
# The design of the virtual machine ends.
# The cracking procedures is below.
# Here is a simple algorithm which costs about 32 bytes in virtual instructions.
defsimple_sort_kernel():
global g_i
global g_a
global g_box
g_i = g_i -1
if g_box[g_a[g_i]] > g_box[g_a[g_i +1]]:
temp = g_a[g_i]
g_a[g_i] = g_a[g_i +1]
g_a[g_i +1] = temp
g_i = g_i +2
# The simple answer needs following upper layer operations, in other words, virtual instructions groups
defload_box_value(): # 3 bytes, we finally use the unpacked version
load_value_i()
load_value_mem()
load_value_box()
defload_array_value(): # 2 bytes, we use the unpacked version
load_value_i()
load_value_mem()
defsave_value_to_op1(): # 1 byte, this operation is atomic
set_op1()
defsave_value_to_op2(): # 1 byte, this operation is atomic
set_op2()
# FIXED means that the instruction cannot be placed after the following FIXED instruction or ahead of the previous FIXED instruction.
# FREE means not FIXED
# The FIXED are both determined by the required function and the minimal size.
defbasic_compare(): # 13 bytes, this operation is not atomic, and has varians, but in minimal size using greedy algorithm.
# Since g_less_than == True is needed for g_box[g_a[op1]] > g_box[g_a[op2]], which makes "exchange" necessary, we have op1 = g_i + 1, op2 = g_i.
# Here op1 is set first, because g_i starts with 1, witch is the second unit of the array.
# of cource one may set op1 first, thus generates variants
load_box_value() # 3 bytes, FIXED
save_value_to_op1() # 1 byte, FIXED
dec() # 1 byte, FIXED
load_box_value() # 3 bytes, FIXED
save_value_to_op2() # 1 byte, FIXED
reset() # 1 byte, FREE, g_less_than == True is necessary for entering any arithmatic operations including the compare operation
load_op(OP_TEST) # 2 bytes, FREE, it can be moved ahead
contitional_calculate() # 1 byte, FIXED
# the load_box_value of basic_compare can be unpacked, so we use the "compare" function below.
defcompare(): # 13 bytes, this operation is not atomic, and has varians, but in minimal size using greedy algorithm.
# Since g_less_than == True is needed for g_box[g_a[op1]] > g_box[g_a[op2]], which makes "exchange" necessary, we have op1 = g_i + 1, op2 = g_i.
# Here op1 is set first, because g_i starts with 1, witch is the second unit of the array.
# of cource one may set op1 first, thus generates variants
load_value_i() # 1 bytes, FIXED
load_value_mem() # 1 bytes, FIXED
load_value_box() # 1 bytes, FIXED
save_value_to_op1() # 1 byte, FIXED
dec() # 1 byte, FIXED
load_value_i() # 1 bytes, FIXED
load_value_mem() # 1 bytes, FIXED
load_value_box() # 1 bytes, FIXED
save_value_to_op2() # 1 byte, FIXED
reset() # 1 byte, FREE, g_less_than == True is necessary for entering any arithmatic operations including the compare operation
load_op(OP_TEST) # 2 bytes, FREE, it can be moved ahead
contitional_calculate() # 1 byte, FIXED
# As we have 2 FREE instruction, which cannot be moved behind the contitional_calculate().
# These 2 FREE instruction has aterable relative orders.
# We have 10 * 11 = 110 variants generated by compare()
defexchange(): # 18 bytes, this operation is not atomic, and has varians, but in minimal size using greedy algorithm.
load_op(OP_XOR) # 2 bytes, FREE, set operation type, it can be downwards
# Of cource in the following blocks, one can set op2 ahead of op1, thus generates 2 * 2 * 2 = 8 variants
load_value_i() # 1 byte, FIXED, g_value = g_i
save_value_to_op1() # 1 byte, FIXED, op1 = g_value
inc() # 1 byte, FREE, g_i = g_i + 1
load_value_i() # 1 byte, FIXED, g_value = g_i
save_value_to_op2() # 1 byte, FIXED, op2 = g_i
contitional_calculate() # 1 byte, FIXED, a[op1] ^= a[op2], which means, a[i] ^= a[i + 1]
save_value_to_op1() # 1 byte, FIXED, op1 = g_value
dec() # 1 byte, FREE, g_i = g_i - 1
load_value_i() # 1 byte, FIXED, g_value = g_i
save_value_to_op2() # 1 byte, FIXED, op2 = g_value
contitional_calculate() # 1 byte, FIXED, a[op2] ^= a[op1], which means, a[i + 1] ^= a[i]
save_value_to_op1() # 1 byte, FIXED, op1 = g_value
inc() # 1 byte, FREE, g_i = g_i + 1
load_value_i() # 1 byte, FIXED, g_value = g_i
save_value_to_op2() # 1 byte, FIXED, op2 = g_value
contitional_calculate() # 1 byte, FIXED, a[op1] ^= a[op2], a[i] ^= a[i + 1]
# In the function "exchange" we have 4 FREE instruction.
# load_op(OP_XOR) can't be put behind or in front of contitional_calculate().
# Neither of inc or dec can be put behind or in front of load_value_i().
# We have amplified the number of the valid cases by a multiplier of 7 because of load_op(OP_XOR).
# We have amplified the number of the valid cases by a multiplier of 2 * 4 * 4 = 32 because of the other 3 FREE instructions
# The answer must contains compare, exchange, and an extra g_i++ for next loop, whose minimum size is 13 + 18 + 1 = 32
# The limited size is 32, so no extra bytes are free and the FIXED is realy fixed!
# So we have 110 * 7 * 32 = 24640 variants.
# Above all, that the space of the answers is very limited is PROVED!
# Here, we use the upper operations to build a default sort kernel, which can be mapped into virtual instructions
defdefault_sort_kernel():
compare()
exchange()
inc()
# Let's test the algorithm!
print(test(default_sort_kernel)
# We get a True! This VERY NORMAL algorithm is the answer to my quiz~
# We get a True! This VERY NORMAL algorithm is the answer to my quiz~
# We get a True! This VERY NORMAL algorithm is the answer to my quiz~
# The following is the robot program seeking for other
answers.
# As the analysis above, we got 6 FREE instructions.
defload_op_test():
load_op(OP_TEST)
# Build all possible "compare" functions
# load_op_test, reset to be added
compare_sequence_base = [load_value_i, load_value_mem, load_value_box, save_value_to_op1, dec, load_value_i, load_value_mem, load_value_box, save_value_to_op2, contitional_calculate]
compare_sequence_list = []
for i inrange(0, 10):
for j inrange(0, 11):
compare_sequence = compare_sequence_base.copy()
compare_sequence.insert(i, load_op_test)
compare_sequence.insert(j, reset)
compare_sequence_list.append(compare_sequence)
# compare_sequence_list is the collection of
defadvanced_compare(compare_sequence):
for i in compare_sequence:
i()
defsort_kernel_of_free_sequence_v1(compare_sequence):
advanced_compare(compare_sequence)
exchange()
inc()
# use the following codes to validate the list
#for i in compare_sequence_list:
# print(test(sort_kernel_of_free_sequence_v1, i))
# recover_box()
defload_op_xor()
load_op(OP_XOR)
# load_op_xor, inc, dec, inc to be added
exchange_sequence_base = [load_value_i, save_value_to_op1, load_value_i, save_value_to_op2, contitional_calculate, \
save_value_to_op1, load_value_i, save_value_to_op2, contitional_calculate, \
save_value_to_op1, load_value_i, save_value_to_op2, contitional_calculate]
exchange_sequence_list = []
for i inrange(0, 7):
for j inrange(9, 13):
for k inrange(4, 8):
for l inrange(1, 3):
exchange_sequence = exchange_sequence_base.copy()
exchange_sequence.insert(l, inc)
exchange_sequence.insert(k, dec)
exchange_sequence.insert(j, inc)
exchange_sequence.insert(i, load_op_xor)
exchange_sequence_list.append(exchange_sequence)
defadvanced_exchange(exchange_sequence):
for i in exchange_sequence:
i()
defsort_kernel_of_free_sequence_v2(compare_sequence, exchange_sequence):
advanced_compare(compare_sequence)
advanced_exchange(exchange_sequence)
inc()
for i in compare_sequence_list:
for j in exchange_sequence_list:
print(test(sort_kernel_of_free_sequence_v2, i, j))
recover_box()
print('Total Count:', len(compare_sequence_list) *len(exchange_sequence_list))
# With compare_sequence_list and exchange_sequence_list, we get all valid sequences!

往期赛题

* 看雪.纽盾 KCTF 2019 Q3 | 第一题点评及解题思路

* 看雪.纽盾 KCTF 2019 Q3 | 第二题点评及解题思路

合作伙伴